Logistic回归实际上是一种分类算法。
假设函数
因为应用于分类问题,想要使得假设函数的值域为[0, 1]。故在线性回归假设函数的基础上,外层再套一个logistic或者叫做sigmoid函数,作为logistic回归的假设函数:
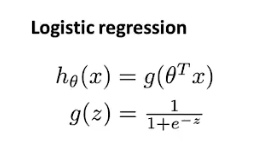
sigmoid函数图型如下:
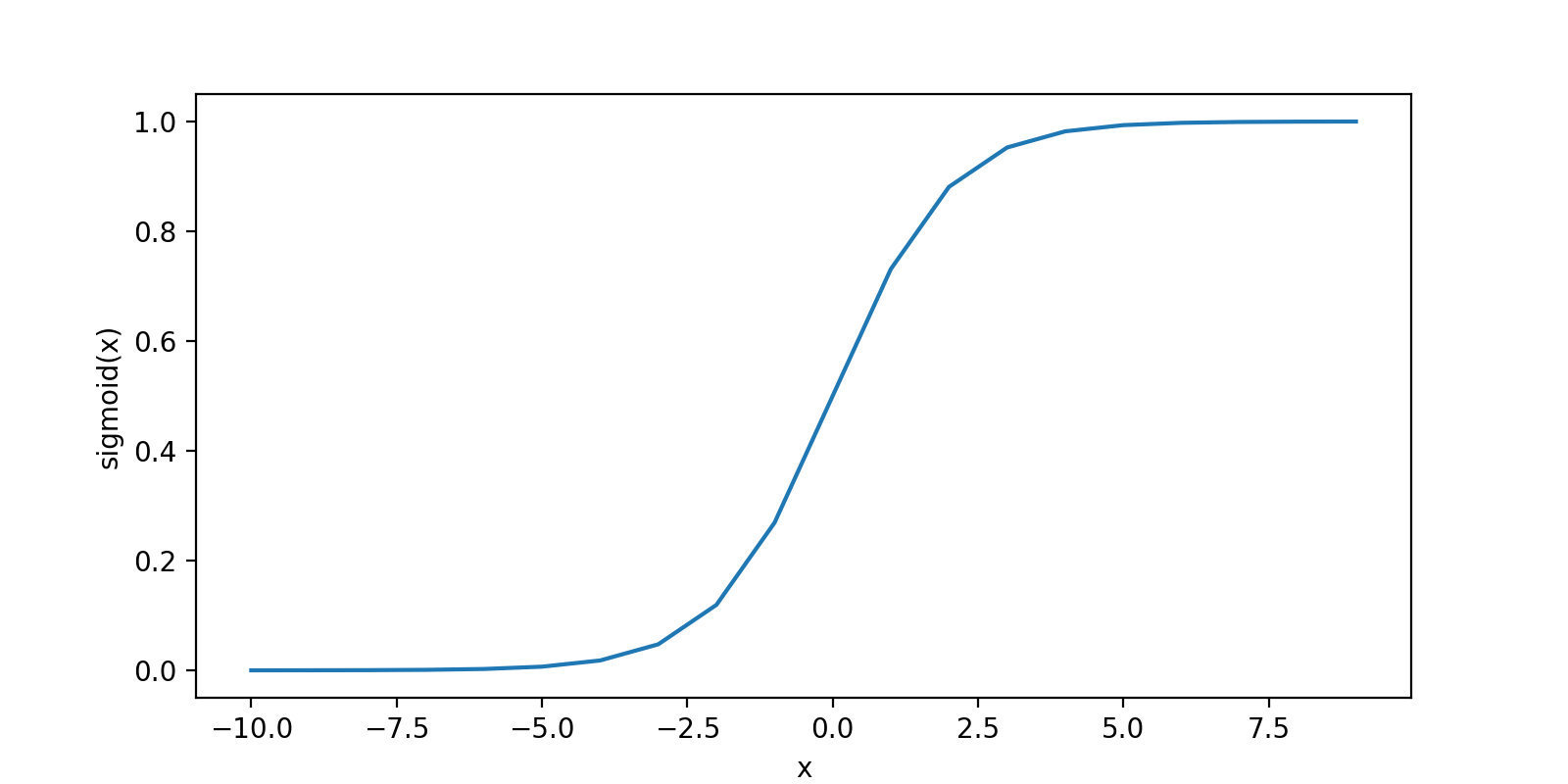
在logistic回归中,假设函数的输出h(x)的含义是当输入x时,预测y=1的可能性。
决策边界
决策边界就是一系列的点连成的线(二元分类),在线上的所有点满足h(x)=0.5,这条线就是决策边界。而这条线将平面分为两个区域,其中一个区域预测y=1(h(x) >= 0.5);另一片区域预测y=0(h(x) < 0.5)。
需要注意的是,决策边界与参数有关,是参数的属性,并不是数据集特征的属性。只要给定了参数向量θ,决策边界也就确定了。
代价函数
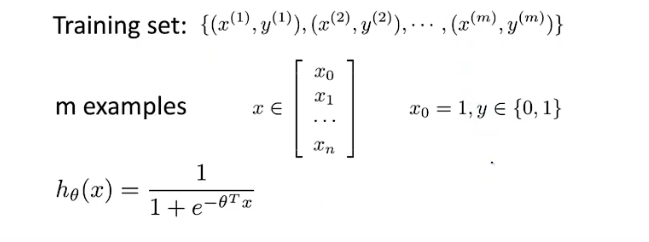
定义Logistic代价函数如下。同时,假设函数h代表了y=1的可能性,所以Cost函数的意义可以解释为:
- 当y=1时,若h预测出的结果趋近于0,那么代价就会趋于无穷;若h预测出的结果趋近于1,那么代价就会趋近于0;
- 当y=0时,若h预测出的结果趋近于1,那么代价就会趋近于无穷;若h预测出的结果趋近于0,那么代价就会趋近于0。

因为y的取值只有0或者1,可以将以上Cost函数进行简化,将两种情况整合到一个式子中去:

梯度下降
我们的目标就是最小化代价函数,利用梯度下降完成此工作。

将代价函数的偏导数算出来,可以发现logistic回归与线性回归中的梯度下降的计算表达式是一致的(两者之间假设函数h不一样)。

高级优化
在最小化最小化代价函数的过程中,每一次算得代价函数J的偏导后,除了进行梯度下降处理,其他的优化策略包括:共轭梯度(Conjugate gradient)、牛顿法(BFGS)、拟牛顿法(L-BFGS)。
这些优化策略的优点在于:无需选择学习率α、比梯度下降算法效率更高。缺点就是这些算法更加的复杂。

多元分类
对于类别大于2的多元分类,同样可以应用logistic回归进行分类。依次令每一种分类定义为y=1,其他所有分类看作是y=0,每一次这样的操作都会产生不同的假设函数h。那么,第i次时产生的假设函数h,就是预测输入为第i个分类的概率。

对于一个新输入的x,选择最大的假设函数h即为对应的预测,即可完成多元分类。