概述
模型
下面展示一个最简单的神经网络,共有三层。第一层称为输入层,最后一层称为输出层,中间层次被称为隐藏层(隐藏层不止一层)
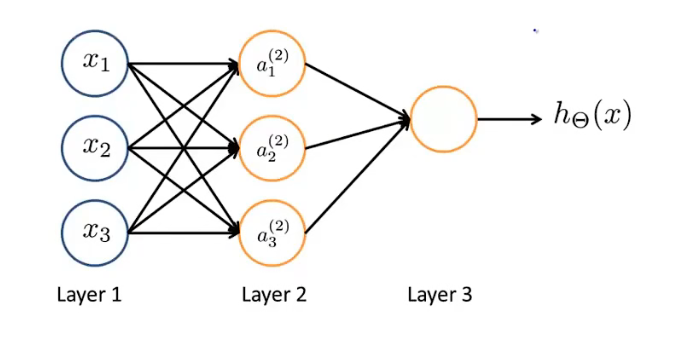
a表示激活项 。Θ表示权重矩阵,它控制从一层到下一层得映射:

以下是激活项的计算公式,其中g代表sigmoid函数。需要注意的是,对于第j层向第j+1层映射的权重矩阵而言,行的数量等于下一层j+1的单元数量,列的数量等于本层j的单元数量+1(因为需要加上偏置单元,x0=1)。

向量化实现
观察在计算激活项时,sigmoid函数的输入可以表示为两向量相乘。利用向量化的方法会使得计算更为简便,以计算第二层为例:
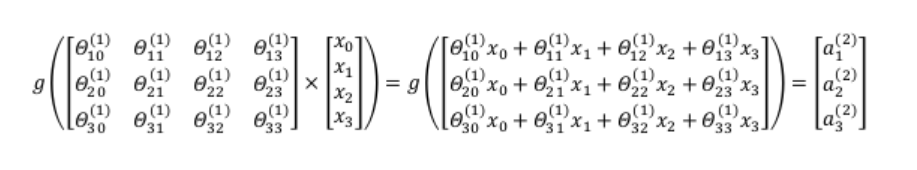
计算输出层:
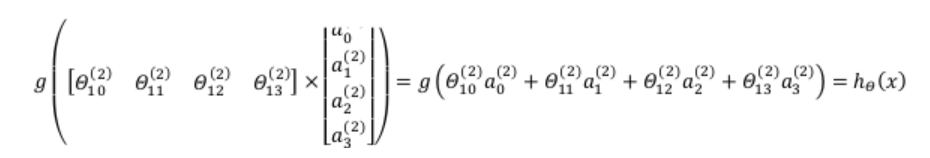
也就是说,每一层所得的得激活项都与上一层相关,这就是前向传播:
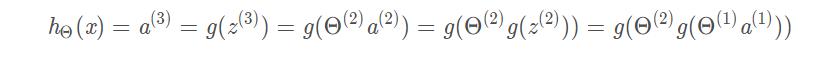
多元分类
在神经网络处理多元分类问题时,其h(x)表示不同的种类。如对图片中的行人、汽车、摩托车和卡车进行识别,h(x)和y都是四维向量。进行二元分类时,只需要一个输出节点,因为一个输出就可以表示0或者1。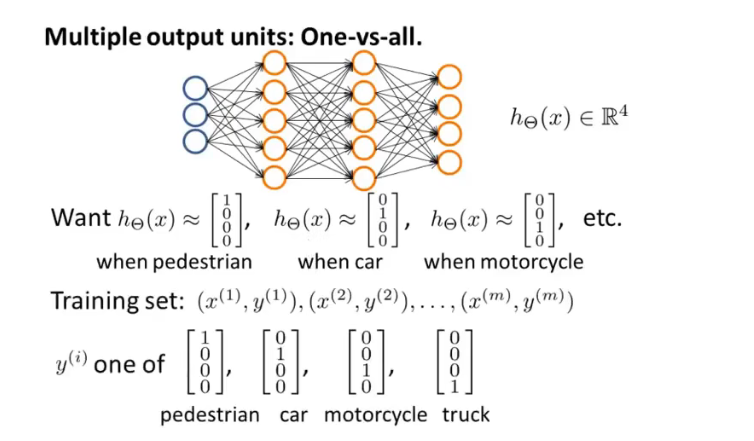
神经网络
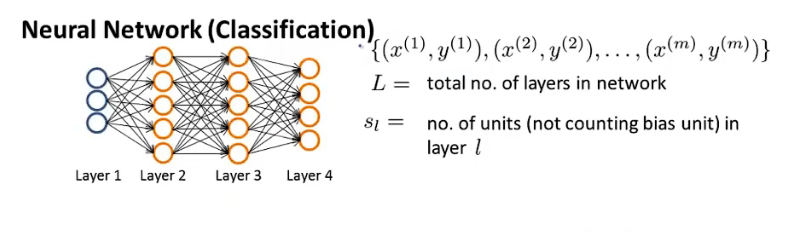
代价函数
与逻辑回归的代价函数形式相似,神经网络的代价函数J如下。同时需要说明的是,第一项相当于神经网络K个输出的代价之和,第二项不包含偏置单元(x0)故从1开始求和。
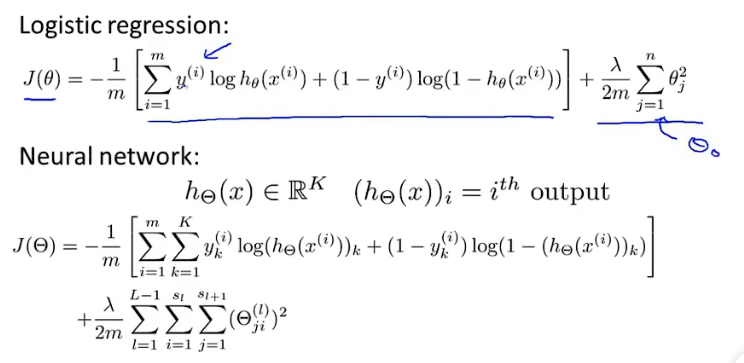
反向传播
反向传播算法,用于代价函数最小化。定义δ为偏差,那么反向传播算法来源于从输出层计算上一层的δ,接着利用上一层的δ计算上上一层的δ项。以此类推,进行反向计算。

我们需要计算代价函数J的偏导数,就需要用到反向传播算法。在得到偏导数之后,就可以通过梯度下降或者其他高级优化算法最小化代价函数了。

梯度检测
当对一个比较复杂的模型(例如神经网络)使用梯度下降算法时,可能会存在一些不容易察觉的错误,意味着,虽然代价看上去在不断减小,但最终的结果可能并不是最优解。
为了避免这样的问题,我们采取一种叫做梯度的数值检验(Numerical Gradient Checking)方法,它能够保证前向传播以及后向传播的正确性(出现错误大部分与反向传播有关)。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。
估计代价函数的导数值
以θ为一个实数的情况下,对梯度的估计采用的方法是在代价函数上选择离θ两个非常近的点,根据这两个点计算导数的估计值。具体来说:
- 双侧差分:若需要估计代价函数J(Θ)上一点θ的导数值,可以通过θ+ε以及θ-ε两点之间连线的斜率来估计θ点的导数值。双侧差分的结果更加准确。
- 单侧差分:通过θ+ε与θ两点之间连线的斜率来估计θ点的导数值。
对于更加一般的情形,当参数有多个即θ为向量时也是类似。

整体流程
梯度检测的整体流程如下:
- 首先通过反向传播计算D(代价函数J的导数)
- 使用梯度数值检测来计算代价函数导数的近似值
- 确保近似值与D非常接近
- 在训练神经网络之前,应当关闭梯度检测
梯度检测是一个计算量非常大的工作,所以在训练神经网络之前应当关闭,否则速度会很缓慢。所以一旦通过检验确定反向传播是正确的,应该关闭它。

随机初始化
在执行梯度下降算法或者其他高级算法时,需要对参数Θ进行初始化。
若用0进行初始化(事实上,若初始化为某个相同的数,也是一样的),对于神经网络而言是不适用的。如下图,每一次更新之后,第二层的激活单元值是相同的。
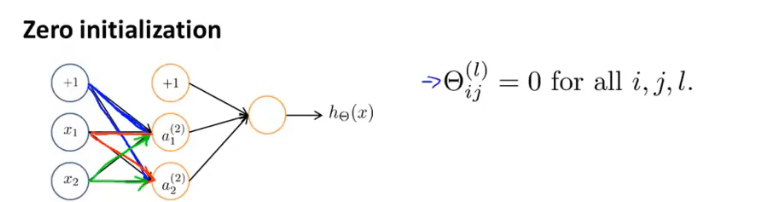
为了解决这个问题,通常采用随机初始化。我们通常初始参数为正负ε之间的随机值。

总结
下面对训练神经网络的过程进行总结
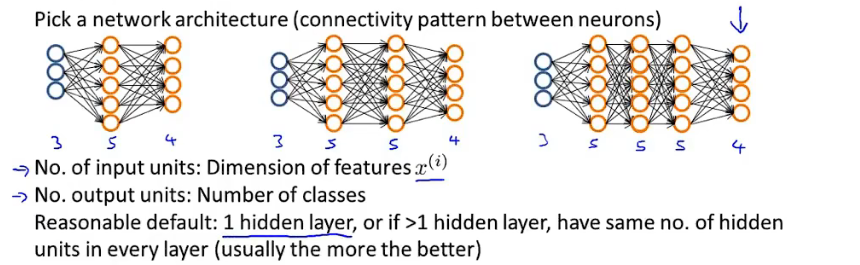
- 首先需要选择一种神经网络结构。输入单元数量就是训练集中特征的数量,输出单元数量就是分类的种数。默认情况下:有1层隐藏层。如果隐藏层数大于1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。
- 训练神经网络:
- 参数随机初始化
- 利用正向传播计算所有的假设函数h
- 编写计算代价函数J的代码
- 利用反向传播计算代价函数的偏导数
- 利用数值检验方法检验这些偏导数,然后关闭梯度检测
- 使用优化算法(如梯度下降)来最小化代价函数