聚类

非监督学习

在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据如下图。在这里我们有一系列点，却没有标签。

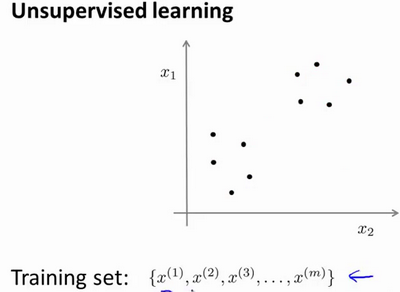
也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到这些点集的算法，就被称为聚类算法。

当然，非监督算法不只是用来分簇，也可以为我们找到其他类型的结构或者其他的一些模式。

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值算法的输入为K（分簇的数量）以及训练集（n维向量，不使用x0=1）。

K-均值算法的流程如下：

首先随机初始化K个聚类中心。
对每一个样本，计算离它最近的聚类中心。
移动每一个聚类中心，将每一个聚类中心移动到这个簇所有点的均值处。如果一个聚类中心所对应的簇中，没有任何一个样本，可以直接移除这个簇，或者重新初始化这个聚类中心。
重复步骤2和3，直到聚类中心不再变化。

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

目标是找到使得代价函数最小的c和μ。在K-均值算法进行每一次迭代时：

在运行K-均值算法的之前，我们首先要随机初始化所有的聚类中心点：

K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

为了解决这个问题，我们通常需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果。这种方法在在K较小（2~10）时是可行的，但是如果K较大，效果不明显。

通常通过人工方法，对聚类数量K进行选择。一个常用的方法是肘部法则：关于肘部法则，就是通过改变K值也就是聚类的类别数量，通过K-均值进行聚类，计算代价函数的大小：

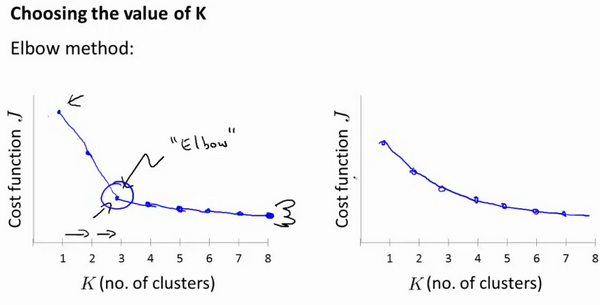
如左图所示，可能会得到像一个人的肘部样式的曲线，到达肘点之前，畸变值下降的非常慢；但是在肘点之后，畸变值下降的非常缓慢。因此，可以选取肘点作为K值。

但是更通常的情况是，会得到一条平滑下降的曲线，如右图所示。一般来说，K值需要根据情况人工的去确定。

无监督学习的第二类问题，就是降维。

主成分分析（Principal Component Analysis，PCA）是最常见的降维算法。

以二维降至一维为例，在PCA中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都投射到该向量上时，我们希望投射误差能尽可能地小，投射误差是从特征向量向该方向向量作垂线的长度。

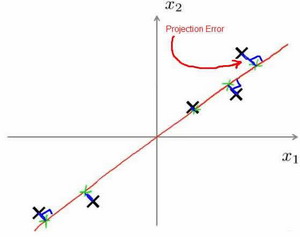
当需要将n维数据降至k维时，就需要找到k个向量，使得总的投射误差最小。

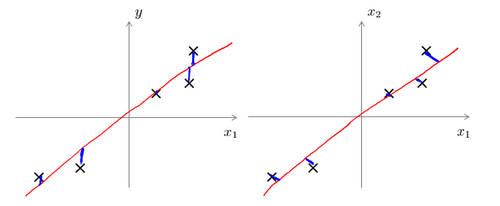
主成分分析 vs 线性回归：

主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差，而线性回归尝试的是最小化预测误差。下图中，左边是线性回归的误差（垂直于横轴），右图是主成分分析的误差（垂直于向量）。