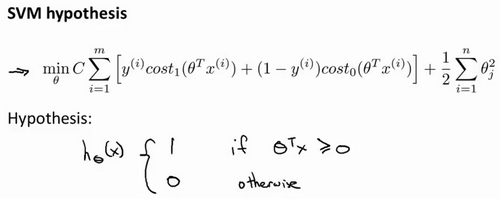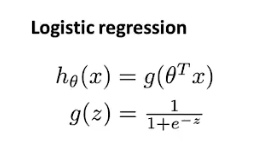支持向量机

目标函数

以下是支持向量机SVM的目标函数，其形式于逻辑回归的形式类似，其中需要注意的是：

• 在SVM中，删除了在逻辑回归里第一项中的1/m。因为1/m仅仅是一个常量，因此，你在这个最小化问题中，无论前面是否有这一项，最终所得到的最优值θ都是一样的。
• 对于逻辑回归的目标函数中，有两项：第一个是训练样本的代价，第二个是我们的正则化项，其形式为A+λB。但是在SVM中，我们将使用一个不同的参数替换这里使用的λ来权衡这两项，其形式为CA+B。因此，在逻辑回归中，如果给定λ一个非常大的值，意味着给予B更大的权重。在SVM中，就对应于将C设定为非常小的值，那么，相应的将会给B比给A更大的权重。
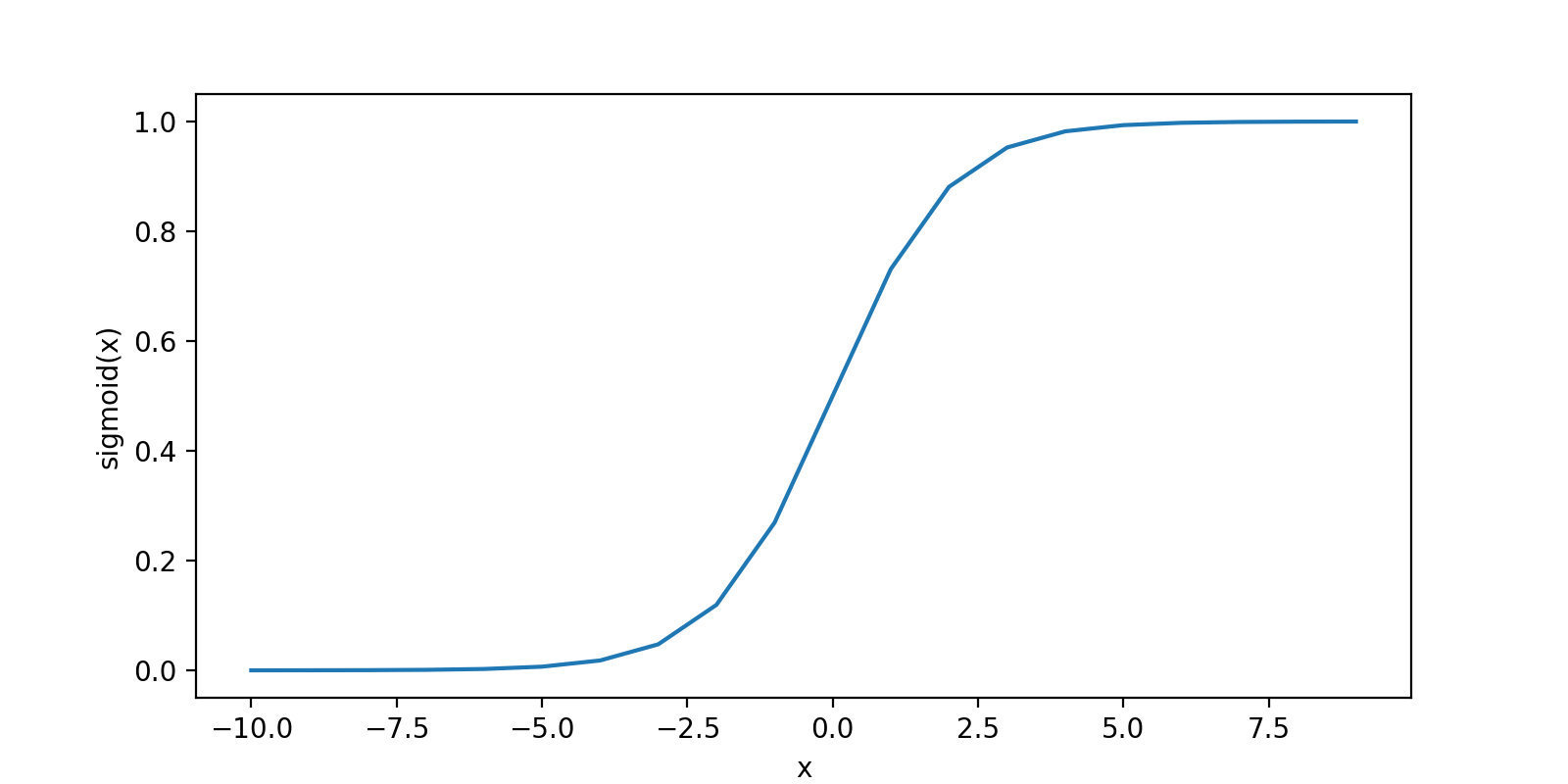
• 在逻辑回归中，输出的是y=1的概率。而在SVM中，当θ^Tx大于等于0时，会输出1，否则输出0

应用及其学习的建议

决定下一步做什么

当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差，我们下一步可以做什么？

• 获得更多的训练样本
• 尝试减少特征的数量，防止过拟合
• 需要更多的特征
• 尝试增加多项式特征
• 减少/增加正则化程度λ

我们不应该随机选择上面的某种方法来改进我们的算法，而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。

概述

模型

下面展示一个最简单的神经网络，共有三层。第一层称为输入层，最后一层称为输出层，中间层次被称为隐藏层（隐藏层不止一层）

a表示激活项 。Θ表示权重矩阵，它控制从一层到下一层得映射：

以下是激活项的计算公式，其中g代表sigmoid函数。需要注意的是，对于第j层向第j+1层映射的权重矩阵而言，行的数量等于下一层j+1的单元数量，列的数量等于本层j的单元数量+1（因为需要加上偏置单元，x0=1）。

欠拟合和过拟合

欠拟合

高偏差：对于样本集，没有很好的拟合训练数据。

过拟合

高方差：如果拟合训练数据过于完美，代价函数J≈0，但是不能很好的预测新的样本，不具备泛化能力。

解决方法：

• 减少特征的数量，但也同时丢失了关于问题的一些信息：

  • 人工的选择保留一些合适的特征
  • 模型选择算法

• 正则化：

  • 保留所有的特征，减少参数θ的数量级或者大小

Logistic回归实际上是一种分类算法。

假设函数

因为应用于分类问题，想要使得假设函数的值域为[0, 1]。故在线性回归假设函数的基础上，外层再套一个logistic或者叫做sigmoid函数，作为logistic回归的假设函数：

sigmoid函数图型如下：

在logistic回归中，假设函数的输出h(x)的含义是当输入x时，预测y=1的可能性。

线性回归

线性回归是一种监督学习算法，我们需要对数据进行预测，以得到一条线性的假设函数h。其中定义函数J为代价函数（Cost Function，也叫代价函数），用于表示对于预测的参数，每一个样本输入值x和它所对应的结果值y之间的差距。我们的目标就是，尽量的优化参数，使得代价函数最小。

定义

一个经典的机器学习定义如下：

A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

比如对于一个垃圾邮件分类程序而言：

• T，识别一封电子邮件是否是垃圾邮件
• E，用户对于邮件的标记是否是垃圾邮件
• P，对垃圾邮件识别的准确率

机器学习算法分类

对于机器学习算法，可以分为：监督学习和非监督学习。简而言之，监督学习就是人为的去教计算机学习一些东西。非监督学习，就是让计算机自己去学习。

监督学习

在监督学习中，对于数据集中的每个样本都带有“正确答案”

• 回归（regression）：预测连续值的输出。
• 分类（classification）：预测离散值的输出。

一个监督学习的基本框架如下：将训练集输入到学习算法中，接着学习算法输出一个假设函数h，假设函数h的作用就是表达x与预测值y的映射关系（在图中，x为房屋的面积，y为预测出可以卖出的价格），简而言之就是进行预测的函数：

无监督学习

在无监督学习中，数据集中的每个样本都没有“正确答案”，要求算法找出数据的类型结构。

• 聚类（cluster）：在无标签的数据集中，其中的样本会天然的呈现出分类的结构，交给无监督学习算法就是去将这些样本自动的划分为不同的类别。

最接近的三数之和

最接近的三数之和

解题思路

首先对数组进行排序，接着遍历数组，用两个指针分别记录nums[i]之后的左右边界，令sum = nums[i]+nums[left]+nums[right]：

• 若sum<target，说明三数之和过小，left++
• 若sum>target，说明三数之和过大，right--

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

func threeSumClosest(nums []int, target int) int {
    // 排序
    sort.Ints(nums)
    // 记录最接近的三叔之和
    closestSum := nums[0]+nums[1]+nums[len(nums)-1]  
    // 遍历数组
    for i := 0; i < len(nums); i++ {
        // 左右指针
        left, right := i+1, len(nums)-1
        for left < right {
            sum := nums[i]+nums[left]+nums[right]   // 三数之和
            if sum == target {
                return target
            } else {
                if abs(target-sum) < abs(target-closestSum) {
                    closestSum = sum
                }
                if sum < target {
                    // 左指针向右移动
                    left++
                } else {
                    // 右指针向左移动
                    right--
                }
            }
        }
    }

    return closestSum
}

func abs(n int) int {
    if n > 0 {
        return n
    }
    return -n
}

二叉树最大宽度

二叉树最大宽度

解题思路

层序遍历，在队列中同时记录每一个节点的位置信息，position值：

• 如果左子树入队，那么左子树的位置信息为2 * position
• 如果右子树入队，那么右子树的位置信息为2 * position + 1

盛最多水的容器

盛最多水的容器

解题思路

1. 暴力解法，双层for循环

2. 双指针法，设立两个指针left和right分别指向左右边界，水槽板高度分别为height[left]和height[right]。那么可容纳水的高度由两个板中的短板决定。在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽底边宽度-1：

   • 若向内移动短板，水槽的短板可能变大，因此下个水槽的面积可能增大
   • 若向内移动长，水槽的短板不变或者变小，因此下个水槽的面积一定减小

   因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。